Review “Attention Is All You Need”

Attention Is All You Need

Attention Is All You Need

서론

BERT, ELECTRA를 접하면서 Transformer라는 단어를 많이 접했다. Transformer를 여러번 배웠지만 정확하게 알고 있지 않은 느낌이 계속 들어서 Transformer 논문을 정리해보려고 한다.

Attention? Attention! 여기에도 설명이 잘 되어 있다. 영어권 사람들은 번역이 필요없으니 추가 내용이 많이 포함되어 있다.

Attention

논문을 읽기 전, 제목에 적혀있는 Attention이 어떤 의미인지 확인했다.

딥러닝을 이용한 자연어 처리 입문에 설명되어 있고 NLP FROM SCRATCH: TRANSLATION WITH A SEQUENCE TO SEQUENCE NETWORK AND ATTENTION에서도 확인할 수 있다.

어텐션(attention): 입력 시퀀스가 길어지면 출력 시퀀스의 정확도가 떨어지는 것을 보정해주기 위한 기법

논문

Abstract

We propose a new simple network architecture, the Transformer, based solely on attention mechanisms, dispensing with recurrence and convolutions entirely.

recurrence와 convolutions는 layer를 의미한다. recurrent layer와 convolutional layer를 제외하고 오로지 Self-Attention Layer만으로 만든 Transformer라는 의미가 된다.

1. Introduction

Attention mechanisms have become an integral part of compelling sequence modeling and trasduction models in various tasks, allowing modeling of dependencies without regard to their distnace in the input or output sequences. In all but a few cases, however, such attention mechanisms are used in conjunction with a recurrent network. In this work we propose the Transformer, a model architecture eschewing recurrence and instead relying entirely on an attention mechanism to draw gloabl dependencies between input and output.

기존의 Attention mechanisms이 사용됐던 한계에 대해 설명하고 Transformer를 제안하고 있다.

2. Background

To the best of our knowledge, however, the Transformer is the transduction model relying entirely on self-attention to compute representations of its input and output without using sequence-aligned RNNs or convolution.

3. Model Architecture

The encoder maps an input sequence of symbol representations $(x_1, …, x_n)$ to a sequence of continuous repesentations $z = (z_1, …, z_n)$. Given z, the decoder then generates an output sequence $(y_1, …, y_m)$ of symbols one element at a time. At each step the model is auto-regressive, consuming the previously generated symbols as additional input when generating the next.

The Transformer follows this overall architecture using stacked self-attention and point-wise, fully connected layers for both the encoder and decoder, shown in the left and right halves of Figure 1, respectively.

x(vector)를 입력받아 encoder에서 z(vector)로 만들어주고, decoder에서는 z를 받아 y(vector)로 출력하게 된다. 그런데 x와 z는 1~n으로 표시되어 있는데 반해 y는 1~m으로 표시되어 있다. 번역을 하게 되면 길이가 달라질 수 있다는 점 때문에 m으로 다르게 표시했다고 추측한다.

Encoder/Decoder

세부 내용 Encoder and Decoder Stacks를 읽기 전, 내가 정확하게 Encoder와 Decoder에 대해 알고 있는 것인지 의문이 들었다. 문장을 입력받는 부분이 encoder, 출력하는 부분이 decoder라는 것은 알지만 RNN에서 정확히 어느 부분이 encoder인지 decoder인지 구분하라고 하면 하지 못 할 것 같다. 그래서 ENCODER/DECODER도 다시 짚고 넘어가기로 했다.

이미지를 찾아봤을 때, 아래처럼 Encoder와 Decoder는 항상 나눠져있다.

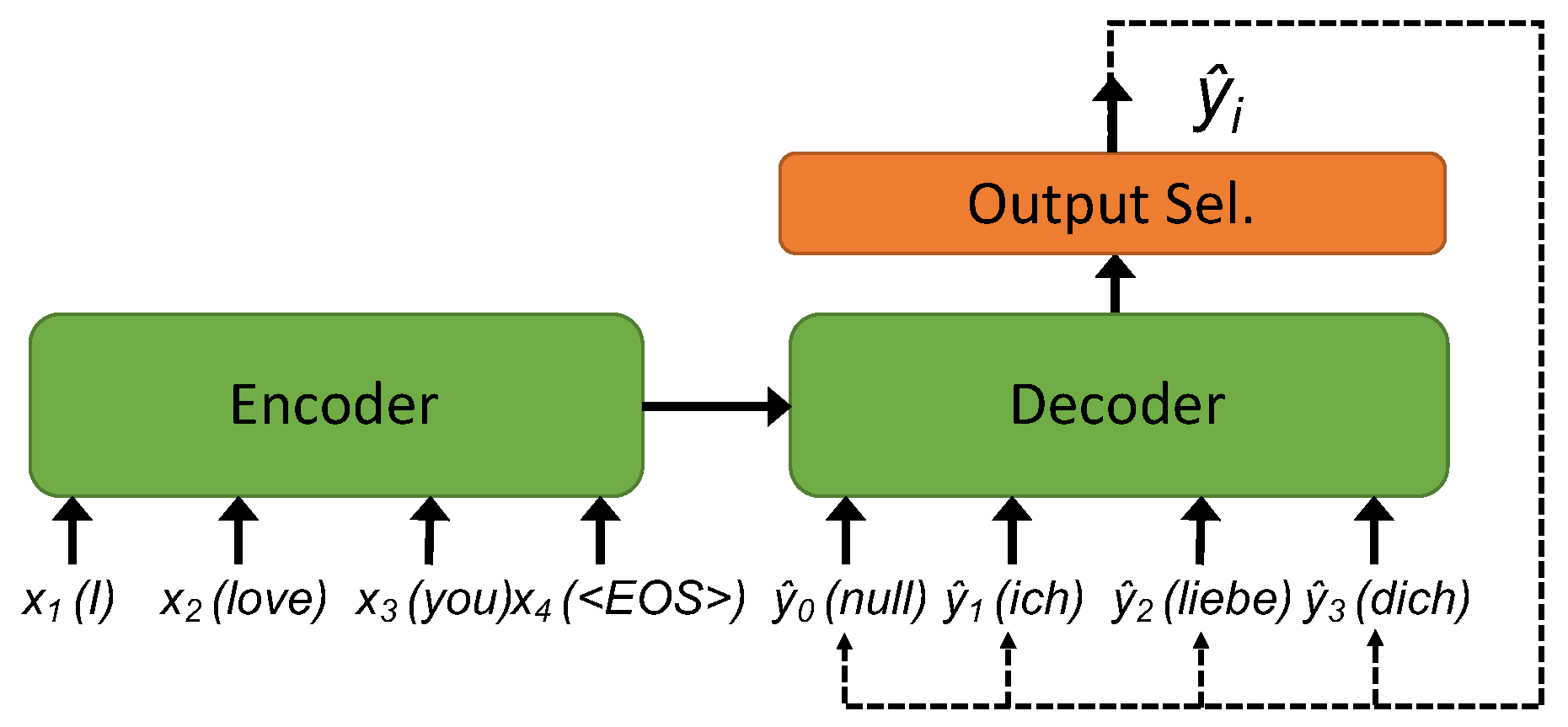
문장을 입력하면 문장이 출력되는 구조에서, 문장을 입력받는 부분이 encoder, 출력하는 부분이 decoder라고 되어있다. 그런데 RNN에서 하나의 입력에 대해 다음 단어를 예상하는 경우가 의문인데 이 때 RNN은 입력을 받기도 하고 출력을 하기도 한다. 그렇다면 encoder와 decoder를 어떻게 나누는 것일까?

위에 적었던 NLP FROM SCRATCH: TRANSLATION WITH A SEQUENCE TO SEQUENCE NETWORK AND ATTENTION 페이지를 보면 EncoderRNN 함수와 DecoderRNN 함수가 구현되어 있다. 코드를 조각내보면 뭐라도 나오겠지.

먼저 EncoderRNN 함수를 보면 super로 nn.Module 함수를 상속받는다. 동일한 명칭으로 IBM github repository에 EncoderRNN과 DecoderRNN 함수가 구현되어 있다. 정작 pytorch 공식 페이지의 rnn 모듈 페이지에 들어가보면 딱히 encoder, decoder가 명시되어 있지 않다.

잘 몰랐던 파이썬 상속

파이썬에서는 부모 클래스의 생성자를 자식 클래스에서 호출하려면 super 함수 내부에 자기 자신의 클래스명으로 호출해줘야 한다. 따라서 pytorch 페이지에 있는 EncoderRNN 클래스 내부에서 super(EncoderRNN, self).__init__()를 정의함으로써 nn.Module 생성자를 호출하는 것이고, IBM github의 함수에서는 super(EncoderRNN, self).__init__() 정의해 자신과 동일한 경로에 존재하는 BaseRNN 클래스의 생성자를 호출하게 된다. 관련 Q&A

(IBM github에 있는) 두 함수를 비교했을 때 확실히 encoder와 decoder는 forward 함수가 return 하는 것부터 달랐다. decoder 함수 부분에는 teacher forcing에 관한 조건도 붙어있다.

3.1 Encoder and Decoder Stacks

Encoder: The encoder is composed of a stack of N = 6 identical layers. Each layer has two sub-layers. The first is a multi-head self-attention mechanism, and the second is a simple, position-wise fully connected feed-forward network. We employ a residual connection around each sub-layers is LayerNorm($x$ + Sublayer($x$)), where Sublayer($x$) is the function implemented by the sub-layer itself. To facilitate these residual connections, all sub-layers in the model, as well as the embedding layers, produce outputs of dimension $d_{model}$ = 512

Decoder: The decoder is also composed of a stack of N = 6 identical layers. In addition to the two sub-layers in each encoder layer, the decoder inserts a third sub-layer, which performs multi-head attention over the output of the encoder stack. Similar to the encoder, we employ residual connections around each of the sub-layers, followed by layer normalization. We also modify the self-attention sub-layer in the decoder stack to prevent positions from attending to subsequent positions. This masking, combined with fact that the output embeddings are offset by one position, ensures that the predictions for position $i$ can depend only on the known outputs at positions less that $i$.

Encoder는 그림에서 설명되어 있는 것처럼 N개의 동일한 layer로 구성되어 있고, 각 layer에는 두 개의 sub-layer가 존재한다. sub-layer는 multi-head self-attention mechanism과 position-wise fully connected feed-forward network로 구성되어 있다. 각 sub-layer에 residual connection을 적용했는데 이 residual connection은 또 ResNet에서 사용한다.

Residual Connection

Skip connection이라고도 불린다.

• 비선형 활성화함수를 통과하지 않고 Gradient가 직접적으로 network를 통해 흐를 수 있도록 함
• ReLU는 본질적으로 비선형이기 때문에 기울기가 폭발하거나 사라
• Residual Connection이 없으면 비선형 활성화 함수를 거친 활성값들에 대해 일일이 선형변환 과정을 거쳐야 하므로 loss 값이 복잡해져 overfitting이 심해짐

그러니까 Transformer architecture에서 Input 이후와 첫 번째 Add & Norm 이후 표시한 2개의 화살표 중 하나는 Feed Forward로 들어가고, 다른 하나는 Feed Forward를 건너뛰고 다시 Add & Norm에 들어가는 부분이 Residual Connection이라는 의미가 된다.

residual connection을 하기 위해 sub-layer의 output dimension을 embedding dimension과 맞춰준다. 그 후 layer normalization을 적용한다.

Decoder는 Encoder와 동일하게 N개의 layer로 구성되어 있고, 각 layer에는 encoder의 2개의 sub-layer에 추가로 encoder의 결과에 multi-head attention 작업을 수행하는 세번째 sub-layer가 들어간다. Encoder와 달리 decoder는 순서가 중요하기 때문에 후속(subsequenct) 위치에 집중하지 않기 위해 self attention sub-layer를 masking을 통해 수정한다. masking은 output embeddings가 한 위치만큼 offset된다는 사실과 결합해 위치 $i$에 대한 예측이 위치 $i$보다 작은 위치에서 알려진 출력에만 의존할 수 있도록 한다.

	I	am	fine	[pad]	[pad]
I		X	X	X	X
am			X	X	X
fine				X	X
[pad]					X
[pad]

위 표에서 X 표시된 부분이 masking된 부분으로 Transformer에서 i번째 값을 예측할 때 앞으로 나오게 될 단어는 가려 예측에 포함되지 않도록 한다.

3.2 Attention

An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.

Attention 함수는 query와 key-value(query, key, value는 전부 vector)를 mapping 해준다. 출력은 values의 가중 합계로 계산되는데 각 값에 할당된 가중치는 query와 해당하는 key의 compatibility function에 의해 계산된다.

Compatibility function은 호환 함수라고 번역되는데 구글링을 해봐도 따로 나오는 관련 자료는 없어 보인다.

Linear compatibility function

선형 호환성 함수-호환성 함수가 아니라 선형 호환성 함수이지만-란 기계 학습 프로그램 (또는 유사한 기술)이 훈련 입력을 검사하여 분류 문제에서 identity를 해결하려고 시도하는 구조적 예측 작업의 일부일 수 있다. 이러한 종류의 구성은 인공 지능을 빠른 클립으로 혁신하는 신경망 모델의 일반적인 프레임워크 내에서 의미가 있다.

선형 호환성 함수는 시스템이 구조화된 생산 작업을 달성하기 위해 이러한 입력 및 출력의 결합된 속성을 인코딩하는 입력/출력 쌍의 공동 피쳐 표현에 유용할 수 있다. 시스템은 주어진 입력 또는 입력 세트에 대해 가장 호환 가능한 결과를 예측할 수 있다. 이러한 유형의 알고리즘 및 수학적 구성은 감독된 머신 러닝에서 구조화 된 예측 결괄르 도출하기 위해 트리 또는 의사 결정 트리 또는 다른 모델을 구문 분석하는 데 적용될 수 있다. 일반적으로 레이블은 프로그램이 식별 결과를 달성하는 데 도움이 된다.

레이블의 유용성은 선형 호환성 함수 및 구조적 예측의 다른 측면에 적용할 때 특히 분명해 보인다.

글 자체가 번역한 것 같다. 설명을 읽어도 compatibility function에 대해 잘 파악되지는 않는다. 이후 알게 된 내용이 있으면 추가할 예정.

3.2.1 Scaled Dot-Product Attention

The input consists of queries and keys of dimension $d_k$, and values of dimension $d_v$. We compute the dot products of the query with all keys, divide each by $\sqrt{d_k}$, and apply a softmax function to obtain the weights on the values.

$ Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V $

The two most commonly used attention functions are additive attention, and dot-product (multi-plicative) attention. Dot-product attention is identical to our algorithm, except for the scaling factor of $\frac{1}{\sqrt{d_k}}$. Additive attention computes the compatibility function using a feed-forward network with a single hidden layer. While the two are similar in theoretical complexity, dot-product attention is much faster and more space-efficient in practice, since it can be implemented using highly optimized matrix multiplication code.

While for small values of $d_k$ the two mechanisms perform similarly, additive attention outperforms dot product attention without scaling for large values of $d_k$. We suspect that for large values of $d_k$, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients. To counteract this effect, we scale the dot products by $\frac{1}{\sqrt{d_k}}$.

input은 $d_k$ 차원의 query, key vector와 $d_v$ 차원의 values vector로 이루어져 있다. Transformer는 모든 query와 key에 대해 dot-products를 계산하고 values의 가중치를 구하기 위해 query와 key에 dot-products를 구한 값을 $\sqrt{d_k}$로 나눠주고 softmax 함수를 적용한다.

Figure 2에 left를 보면 잘 설명되어 있는데 Q와 K를 dot-product 해주고, $\sqrt{d_k}$로 Scale을 해준다는 의미다.

가장 많이 사용되는 두 가지 attention은 additive attention과 dot-product attention이다.

• Dot-product attention: scaling factor가 $\frac{1}{\sqrt{d_k}}$인 점만 제외하면 Transformer에서 사용하는 알고리즘과 동일하다.
• Additive attention: 하나의 hidden layer가 포함된 feed-forward network를 이용해 compatibility function을 계산한다. 위 두 attention은 이론상 복잡성이 비슷하지만 dot-product attention은 highly optimized된 행렬 곱셈 코드를 사용하여 구현할 수 있기 때문에 additive attention에 비해 훨씬 빠르고 공간 효율이 좋다.

$d_k$ 값이 작은 경우 두 attention의 성능은 비슷하지만 additive attention은 $d_k$에 대한 scaling을 하지 않기 때문에 dot product에 비해 성능이 좋게 나온다. $d_k$의 값이 큰 경우 내적의 크기가 커져 softmax 함수에서 극히 작은 기울기로 계산되기 때문이라고 생각하여 이 효과를 막기 위해 내적을 $\frac{1}{\sqrt{d_k}}$ 값으로 scaling 해준다.

3.2.2 Multi-Head Attention

Instead of performing a single attention function with $d_{model}$-dimensional keys, values and queries, we found it beneficial to linearly project the queries, keys and values $h$ times with differenct, learned linear projections to $d_k$, $d_k$ and $d_v$ dimensions, respectively. On each of these projected versions of queries, keys and values we then perform the attention function in parallel, yielding $d_v$-dimensional output values. Theses are concatenated and once again projected, resulting in the final values, as depicted in Figure 2.

Multi-head attention allows the model to jointly attend to information from different representation subspaces at different positions. With a single attention head, averaging inhibits this.

$ MultiHead(Q, K, V) = Concat(head_1, …, head_h)W^O$ where $head_i = Attention(QW^Q_i, KW^k_i, VW^V_i) $

Where the projections are parameter matrices $W^Q_i \in R^{d_{model} \times d_k}, W^K_i \in R^{d_{model} \times d_k}, W^V_i \in R^{d_model \times d_v}$ and $W^O \in R^{hd_v \times d_{model}}$.

In this work we employ $h$ = 8 parallel attention layers, or head. For each of these we use $d_k = d_v = d_{model} / h = 64$. Due to the reduced dimension of each head, the total computational cost is similar to that of single-head attention with full dimensionality.

$d_{model}$-dimensional의 keys, values, queries를 하나의 attention으로 처리하는 것보다 queries, keys, values를 $d_k$로 학습된 linearly project을 각각 $h$번 linear project하는 것이 유리하다.

각 projected된 queires, keys, values들을 병렬로 attention을 수행하여 $d_v$ 차원의 output 값을 산출한다. Figure2를 보면 concat되고 다시 project되어 최종 값이 생성되는 것을 확인할 수 있다.

Multi-head attention을 사용하면 모델이 서로 다른 positions에 있는 서로 다른 representation subspaces의 정보에 공동으로 집중할 수 있다. Single attention head는 averaging이 이를 억제한다.

수식에서 $MultiHead(Q, K, V)$는 각각의 $head_i$를 concat한 값과 $W^O$를 곱해준다. 이 때 각각의 vector를 곱해주는 가중치는 별개로 $W^Q_i \in R^{d_{model} \times d_k}, W^K_i \in R^{d_{model} \times d_k}, W^V_i \in R^{d_model \times d_v}$ and $W^O \in R^{hd_v \times d_{model}}$로 정의되어 있다. 각기 다른 Weight를 사용하게 되는 것이다. W^O는 output에 대한 parameter matrix.

각 head의 크기가 줄어들기 때문에 총 계산 비용은 full dimensionality의 single-head attention(3.2.2 가장 첫 문장에 적은 $d_{model}$-dimensional의 keys, values, queries를 하나의 attention으로 처리하는 것)과 비슷하다.

MultiheadAttention

• pytorch MultiheadAttention Doc
• pytorch MultiheadAttention sourcecode
• huggingface transformer MultiHeadAttention sourcecode

두 코드의 차이가 무엇인지 확인해봤는데 예전에는 Pytorch의 공식 MultiheadAttention class가 없었던 것처럼 보인다.

3.2.3 Applications of Attention in our Model

The Transformer uses multi-head attention in three different ways:

• In “encoder-decoder attention” layers, the queries come from the previous decoder layer, and the memory keys and values come from the output of the encoder. This allows every position in the decoder to attend over all input sequence. This mimics the typical encoder-decoder attention mechanisms in sequence-to-sequence models.
• The encoder contains self-attention layers. In a self-attention layer all of the keys, values and queries come from the same place, in this case, the output of the previous layer in the encoder. Each position in the encoder can attend to all positions in the previous layer of the encoder.
• Similarly, self-attention layers in the decoder allow each position in the decoder to attend to all positions in the decoder up to and including that position. We need to prevent leftward information flow in the decoder to preserve the auto-regressive property. We implement this inside of scaled dot-product attention by masking out (setting to - $\infty$) all values in the input of the softmax which correspond to illegal connections.

Transformer는 multi-head attention을 세가지 방법으로 사용한다.

• “encoder-decoder attention” layer에서 queries는 이전의 decoder layer에서 생성되고, memory keys와 values는 encoder의 output에서 생성된다. decoder의 모든 position에서 모든 input sequence(encoder의 output)에 집중(attend)하게 된다. sequence-to-sequence 모델의 전형적인 encoder-decoder attention mechanism을 흉내낸 것이다. 아래 그림에서 Multi-Head Attention 부분을 설명하고 있다.

• encoder는 self-attention layers를 포함하고 있다. self-attention layer에서 모든 keys, values와 queries는 같은 곳-이 경우 encoder의 이전 layer의 output-에서 생성된다. encoder의 각 position은 encoder의 이전 layer의 모든 위치에 attend 할 수 있다. 아래 그림에서 Multi-Head Attention에 들어가는 keys, values와 queries는 이전 layer인, Input Embedding에서 Positional Encoding을 거친 output 값이 된다.

• decoder의 self-attention도 비슷하게 decoder의 각 위치(position)이 해당 위치를 포함하여 decoder의 모든 위치에 집중(attend)할 수 있게 한다. auto-regressive 속성을 유지하기 위해 decoder의 leaftward 정보 흐름을 방해해야 한다. illegal connections에 해당하는 softmax의 입력에서 모든 값을 masking(setting to - $\infty$)하여 scaled dop-product(내적)을 적용한다. decoder에서는 self attention을 할 때 3.1의 masking된 부분처럼 참조하면 안 되는 값(X 값들: 미래를 보고 미래를 예측하는 경우)을 제외해주어야 한다. Decoder의 앞선 시점들의 hidden layer들만 사용할 수 있게 만들어야 한다는 의미. illegal connection은 Mask를 통해 -inf 값을 주게 되면 softmax에서 값이 0이 되어 attend를 못하도록 구현하고 있다고 한다.

3.3 Position-wise Feed-Forward Networks

In addition to attention sub-layers, each of the layers in our encoder and decoder contains a fully connected feed-forward network, which is applied to each position separately and identically. This consists of two linear transformations with a ReLU activation in between.

$ FFN(x) = max(0, xW_1 + b_1)W_2 + b_2 $

While the linear transformations are the same across different positions, they use different parameters from layer to layer. Another way of describing this is as two convolutions with kernel size 1. The dimensionality of input and output is $d_{model} = 512$, and the inner-layer has dimensionality $d_{ff} = 2048$”.

attention sub-layer에 추가로 encoder와 decoder의 각 layer는 각 위치(position)에 개별적으로 동일하게 적용된 fully connected feedd-forward network를 포함하고 있다. 사이에 ReLU 활성 함수를 둔 두 개의 linear transformations로 구성되어 있다.

이미지 출처

위 그림에서 잘 설명해주는데 초록색 박스의 가로가 문장 길이, 세로가 One-hot vector를 크기로 갖는 행렬이라고 글에서 설명해준다.

식에서 $max(0, xW_1 + b_1)$ 부분은 $x$가 input, $W_1$은 첫 번째 Fully-Connected Layer, $W_2$가 두 번째 Fully-Connected Layer가 된다고 생각한다. linear transformation을 표현할 때 $Wx + b$의 형태고 $max(0, f_{bef})$의 표현은 ReLU 활성함수 표현식이다.

linear transformations는 다른 위치에서는 동일하지만 layer마다 다른 매개 변수를 사용한다. 이를 설명하는 또 다른 방법은 input과 output의 차원은 $d_{model} = 512$이고 inner-layer의 차원은 $d_{ff} = 2047$인 상태에서 커널 크기가 1인 convolution을 두 번 수행한 것.

3.4 Embeddings and Softmax

Similarly to other sequence transduction models, we learned embeddings to convert the input tokens and output tokens to verctors of dimension $d_{model}$. We also use the usual learned linear transformation and softmax function to convert the decoder output to predicted next-token probabilities. In our model, we share the same weight matrix between the two embedding layers and the pre-softmax linear transformation. In the embedding layers, we muliply those weights by $\sqrt{d_{model}}$.

다른 sequence 모델과 마찬가지로 입력 토큰과 출력 토큰을 $d_{model}$ 차원의 vector로 변환하는 embedding을 배웠다. 또한 일반적인 linear transformation과 softmax 함수를 사용하여 decoder의 출력을 예측된 next-token 확률로 변환한다. Transformer에서는 두 개의 embedding layer와 pre-softmax linear transformation 간에 동일한 가중치 행렬을 공유한다. embedding layer에서 $\sqrt{d_{model}}$로 가중치들을 곱해준다.

3.5 Positional Encoding

Since our model contains no recurrence and no convolution, in order for the model to make use of the order of the sequence, we must inject some information about the releative or absolute position of the tokens in the sequence. To this end, we add “positional encodings” to the input embeddings at the bottoms of the encoder and decoder stacks. The positional encodings have the same dimension $d_{model}$ as the embeddings, so that the two can be summed. There are many choices of positional encodings.

In this work, we use sine and cosine functions of different frequencies:

$PE_{(pos, 2i)} = sin(pos/10000^{2i/d_{model}})$ $PE_{(pos, 2i+1)} = cos(pos/10000^{2i/d_{model}})$

where $pos$ is the position and $i$ is the dimension. That is, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from 2$\pi$ to 10000 $\cdot$ 2$\pi$. We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k$, $PE_{pos+k}$ can be represented as a linear function of $PE_{pos}$.

We also experimented with using learned positional embeddings instead, and found that the two versions produced nearly identical results. We chose the sinusoidal version becasue it may allow the model to extrapolate to sequence lengths longer than the ones encountered during training.

| Layer Type | Complexity per Layer | Sequential Operations | Maximum Path Length | |:———-:|:——————–:|:———————:|:——————-:| |Self-Attention | $O(n^2 · d)$ | $O(1)$ | $O(1)$ | |Recurrent | $O(n · d^2)$ | $O(n)$ | $O(n)$ | |Convolutional | $O(k · n · d^2)$ | $O(1)$ | $O(log_k(n))$ | |Self-Attention (restricted) | $O(r · n · d)$ | $O(1)$ | $O(n/r)$ | Table 1: Maximum path lengths, per-layer complexity and minimum number of sequential operations for different layer types. n is the sequence length, d is the representation dimension, k is the kernel size of convolutions and r the size of the neighborhood in restricted self-attention.

Transformer에는 recurrence와 convolution이 없기 때문에 sequence 순서를 사용하기 위해선 sequence token의 상대 또는 절대 위치의 정보를 넣어줘야 한다. 이를 위해 encoder와 decoder 하단의 stack에 있는 input embeddings에 “positional encodings”을 추가해준다. positional encodings는 embedding와 동일한 차원인 $d_{model}$ 차원을 가지기 때문에 둘을 더해줄 수 있다. positional encodings로 선택할 수 있는 방법이 많은데 자세한 내용은 논문.

논문에서는 다른 주기의 sine, cosine 함수를 사용한다.

식에서 $pos$는 위치, $i$는 차원이다. positional encoding의 각 차원은 sinusoid에 해당한다. 파장은 2$\pi$에서 10000 $\cdot$2 $\pi$까지 기하학적 진행을 형성한다. 고정된 offset $k$에서 $PE_{pos+k}$는 $PE_{pos}$의 선형 함수(linear function)로 표현할 수 있기 때문에 이 함수가 모델이 상대 위치로 쉽게 배울 수 있다고 판단해 이 함수를 선택했다고 설명한다.

learned positional embedding를 대신 사용하여 시험했을 때 두 버전이 거의 동일한 결과를 출력했다. sinusoidal 버전을 선택한 이유는 모델이 훈련 중에 만나는 길이보다 긴 sequece 길이를 extrapolate(보외법)할 수 있기 때문이다.